Aplicaciones de la Ley de Gauss

 QUE ES UN CONDENSADOR?? (VIDEO)

INTERESANTISIMO !!

CONDENSADORES

TIPOS DE CONDENSADORES O CAPACITORES

Condensador eléctrico - Capacitor eléctrico

---

En condensador eléctrico es un dispositivo formado por dos placas metálicas separadas por un aislante llamado dieléctrico.

Un dieléctrico o aislante es un material que evita el paso de lacorriente.

El condensador eléctrico o capacitor eléctrico almacena energía en la forma de un campo eléctrico (es evidente cuando el capacitor funciona con corriente directa) y se llama capacitancia o capacidad a la cantidad de cargas eléctricas que es capaz de almacenar

La capacidad depende de las características físicas delcondensador:

- Si el área de las placas que están frente a frente es grande la capacidad aumenta

- Si la separación entre placas aumenta, disminuye la capacidad

- El tipo de material dieléctrico que se aplica entre las placas también afecta la capacidad

- Si se aumenta la tensión aplicada, se aumenta la carga almacenada.

Dieléctrico o aislante del condensador eléctrico

Un dieléctrico o aislante es un material que evita el paso de la corriente, y su función es aumentar la capacitancia del capacitor.

Los diferentes materiales que se utilizan como dieléctricos tiene diferentes grados depermitividad (diferente capacidad para el establecimiento de un campo eléctrico

Mientras mayor sea la permitividad, mayor es la capacidad del condensador eléctrico.

La unidad de medida es el faradio. Hay submúltiplos como el miliFaradio (mF), microFaradio (uF), el nanoFaradio (nF) y el picoFaradio (pF)

Las principales características eléctricas de un condensador son su capacidad o capacitancia y su máxima tensión entre placas (máxima tensión que es capaz de aguantar sin dañarse).

Nunca conectar un capacitor eléctrico a un voltaje superior
al que puede aguantar, pues puede explotar

MIRA ESTE VIDEO"BREVE"  ACERCA DE GAUSS ( SU VIDA)

.

QUIÉN  ERA GAUSS.....?

SU BIOGRAFIA:

Johann Karl Friedrich Gauss  (Gauß) (?·i) (Brunswick, 30 de abril de 1777 – Gotinga, 23 de febrero de 1855), fue unmatemático, astrónomo, geodesta, y físico alemán que contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la estadística, el álgebra, la geodesia, el magnetismo y la óptica. Considerado «el príncipe de los matemáticos» y «el matemático más grande desde la antigüedad», Gauss ha tenido una influencia notable en muchos campos de la matemática y de la ciencia, y es considerado uno de los matemáticos que más influencia ha tenido en la Historia. Fue de los primeros en extender el concepto de divisibilidad a otros conjuntos.

Gauss pronto fue reconocido como un niño prodigio, pese a provenir de una familia campesina de padres analfabetos; de él existen muchas anécdotas acerca de su asombrosa precocidad. Hizo sus primeros grandes descubrimientos mientras era apenas un adolescente en el bachillerato y completó su magnum opus, Disquisitiones arithmeticae a los veintiún años (1798), aunque fue publicado en 1801. Fue un trabajo fundamental para que se consolidara la teoría de los números y ha moldeado esta área hasta los días presentes.

Juventud

Johann Carl Friedrich Gauss nació en el ducado de Brunswick, Alemania, el 30 de abril de 1777, en una familia campesina muy pobre: su abuelo era un humilde jardinero y repartidor. Su padre nunca pudo superar la espantosa miseria con la que siempre convivió. De pequeño Gauss fue respetuoso y obediente, y ya en su edad adulta nunca criticó a su padre, quien murió poco después de que Gauss cumpliera 30 años, por su rudeza y violencia para con él.

Desde muy pequeño, Gauss mostró su talento para los números y para el lenguaje. Aprendió a leer solo y, sin que nadie lo ayudara, aprendió muy rápido la aritmética elemental desde muy pequeño. En 1784, a los siete años de edad, ingresó a una de las escuelas de primeras letras de Brunswick donde daba clases un maestro rural llamado Büttner, quien corrigió rápidamente su lectura, le enseñó gramática, ortografía y caligrafía y perfeccionó su talento matemático y lo animó a continuar el bachillerato, como consta en su carta para que lo aceptaran en el Lyceum; pero que usaba unos métodos severos y una estricta disciplina, lo que desagradaba a alguien tan sensible. Se cuenta la anécdota de que, a los dos años de estar en la escuela, durante la clase de Aritmética, el maestro propuso el problema de sumar los números de una progresión aritmética.¹ Gauss halló la respuesta correcta casi inmediatamente diciendo «Ligget se'» ('ya está'). Al acabar la hora se comprobaron las soluciones y se vio que la solución de Gauss era correcta, mientras que no lo eran muchas de las de sus compañeros.

A los 12 años ya miraba con cierto recelo los fundamentos de la geometría, A los 14 años, fue presentado ante el duque de Brunswick. Este quedó fascinado por lo que había oído del muchacho, y por su modestia y timidez, por lo que decidió hacerse cargo de todos los gastos de Gauss que permitió asegurar que su educación en el bachillerato llegara a buen fin. Allí conoció al matemático Martin Bartels quien fue su profesor y se aceleraron sus progresos en Matemáticas. Ambos estudiaban juntos, se apoyaban y se ayudaban para descifrar y entender los manuales que tenían sobre álgebra y análisis elemental. En estos años se empezaron a gestar algunas de las ideas y formas de ver las matemáticas, que caracterizaron posteriormente a Gauss. Se dio cuenta, por ejemplo, del poco rigor en muchas demostraciones de los grandes matemáticos que le precedieron, como Newton, Euler,Lagrange y otros más.

Al año siguiente de conocer al duque, Gauss ingresó al Collegium Carolinum para continuar sus estudios, y lo que sorprendió a todos fue su facilidad para las lenguas. Aprendió y dominó el griego y el latín en muy poco tiempo. Estuvo tres años en el Collegium y, al salir, no tenía claro si quería dedicarse a las matemáticas o a la filología. En esta época ya había descubierto su ley de los mínimos cuadrados, lo que indica el temprano interés de Gauss por la teoría de errores de observación y su distribución.

A los 17 tuvo sus primeras ideas intuitivas sobre la posibilidad de otro tipo de geometría. A los 18 años, Gauss se dio a la tarea de completar lo que, a su juicio, habían dejado sin concluir sus predecesores en materia de teoría de números. Así descubrió su pasión por la aritmética, área en la que poco después tuvo sus primeros triunfos. Su gusto por la aritmética prevaleció por toda su vida, ya que para él «La matemática es la reina de las ciencias y la aritmética es la reina de las matemáticas».

Madurez

Distribución normal

En 1796 demostró que se puede dibujar un polígono regular de 17 lados con regla y compás.

Fue el primero en probar rigurosamente el teorema fundamental del álgebra (disertación para su tesis doctoral en 1799), aunque una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente.

En 1801 publicó el libro Disquisitiones arithmeticae, con seis secciones dedicadas a la Teoría de números, dándole a esta rama de las matemáticas una estructura sistematizada. En la última sección del libro expone su tesis doctoral. Ese mismo año predijo la órbita de Ceres aproximando parámetros por mínimos cuadrados.

En 1809 fue nombrado director del Observatorio de Gotinga. En este mismo año publicó Theoria motus corporum coelestium in sectionibus conicis Solem ambientium describiendo cómo calcular la órbita de un planeta y cómo refinarla posteriormente. Profundizó sobre ecuaciones diferenciales y secciones cónicas.

Gauss murió en Gotinga el 23 de febrero de 1855.

La primera estancia de Gauss en Gotinga duró tres años, que fueron de los más productivos de su vida. Regresó a su ciudad natal Brunswick a finales de 1798 sin haber recibido ningún título en la Universidad, pero en ese momento su primera obra maestra,Disquisitiones arithmeticae, estaba casi lista aunque no se publicó por primera vez hasta 1801.

Este libro, escrito en latín, está dedicado a su mecenas, el duque Ferdinand, por quien Gauss sentía mucho respeto y agradecimiento. Es un tratado de la teoría de números en el que se sintetiza y perfecciona todo el trabajo previo en esta área. La obra consta de 8 capítulos pero el octavo no se pudo imprimir por cuestiones financieras. El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y a coeficientes complejos, tiene tantas raíces como su grado.

Contribuciones a la Teoría del Potencial

El Teorema de la divergencia de Gauss, de 1835 y publicado apenas en 1867, es fundamental para la teoría del potencial y la física. Coloca en un campo vectorial la integral del volumen para la divergencia de un campo vectorial en relación con la integral de superficie del campo vectorial alrededor de dicho volumen.

LA LEY DE GAUSS

trabajo eléctrico

Trabajo realizado por el campo eléctrico

El trabajo que realiza el campo eléctrico sobre una carga q cuando se mueve desde una posición en el que el potencial es V_A a otro lugar en el que el potencial es V_B es

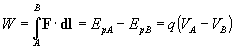
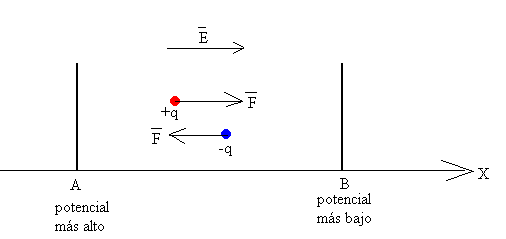
• El campo eléctrico realiza un trabajo W cuando una carga positiva q se mueve desde un lugar A en el que el potencial es alto a otro B en el que el potencial es más bajo. Si q>0 y V_A>V_B entonces W>0.
• El campo eléctrico realiza un trabajo cuando una carga negativa q se mueve desde un lugar B en el que el potencial es más bajo a otro A en el que el potencial es más alto.
   
• Una fuerza externa tendrá que realizar un trabajo para trasladar una carga positiva q desde un lugar B en el que el potencial es más bajo hacia otro lugar A en el que el potencial más alto.
• Una fuerza externa tendrá que realizar un trabajo para trasladar una carga negativa q desde un lugar A en el que el potencial es más alto hacia otro lugar B en el que el potencial más bajo.

http://www.sc.ehu.es/sbweb/fisica/elecmagnet/campo_electrico/campo/campo.htm

_____________     ______________________



OTRO APORTE:

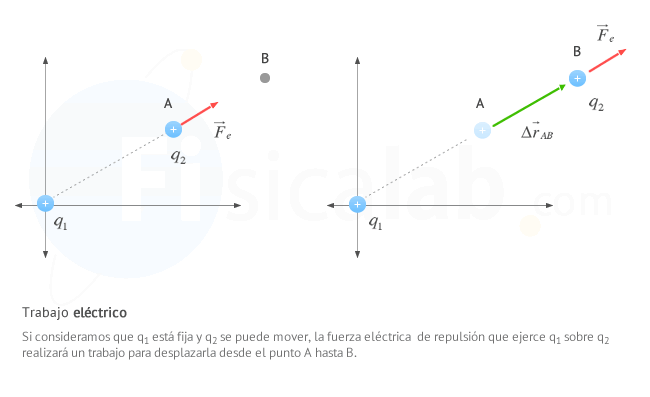
El trabajo eléctrico es el trabajo que realiza una fuerza eléctrica sobre una carga que se desplaza desde un punto A hasta otro punto B.

Si suponemos que la fuerza es constante durante todo el desplazamiento, se puede expresar de la siguiente forma:

W⃗ e(A→B)=F⃗ e⋅Δr⃗ AB

donde:

• W⃗ e(A→B) es el trabajo eléctrico. En el S.I. se mide en Julios (J).
• F⃗ e es la Fuerza eléctrica que sufre la carga. En el S.I. se mide en Newtons (N).
• Δr⃗ AB es el vector desplazamiento entre ambos puntos. En el S.I. se mide en metros (m).

Al igual que ocurre con otras fuerzas, como la fuerza gravitatoria, la fuerza eléctrica es una fuerza conservativa. Esto implica que:

• El trabajo que realiza una fuerza eléctrica para mover un cuerpo cargado desde una posición A hasta otra B, únicamente depende de dichas posiciones y no del camino seguido para llegar de A a B.
• Cuando el camino que sigue el cuerpo entre A y B es un camino cerrado o un ciclo, el trabajo eléctrico es nulo.

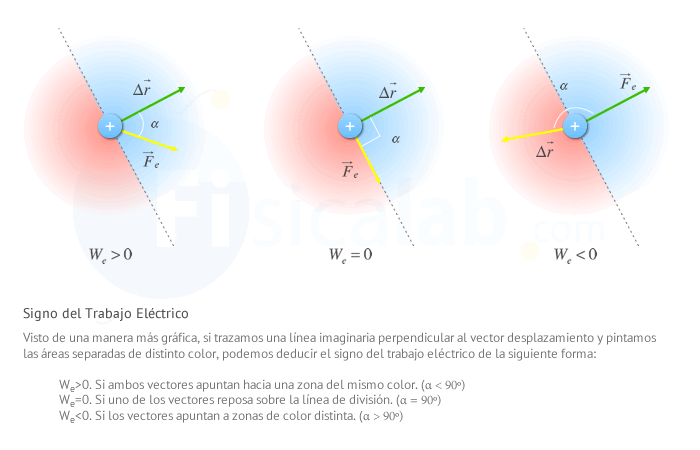
Signo del Trabajo Eléctrico

Si nos atenemos a la expresión matemática de trabajo eléctrico, nos damos cuenta de que la operación principal es unproducto escalar. Esta operación puede devolver un valor positivo, negativo o nulo, dependiendo del menor ángulo que se forme entre la fuerza eléctrica y el vector desplazamiento. Si el ángulo (α) es:

• α > 90º. El trabajo eléctrico será negativo (We < 0).
• α = 90º. El trabajo eléctrico será nulo (We = 0).
• α < 90º. El trabajo eléctrico será positivo (We > 0).

¿Cómo podemos interpretar este signo?. A priori, si un cuerpo cargado se encuentra libre y derrepente sufre la acción de una fuerza eléctrica, el cuerpo se moverá en el sentido de la fuerza eléctrica y por tanto, el trabajo eléctrico será positivo. 

Si por el contrario, se le aplica una fuerza externa contraria a la fuerza eléctrica que provoca un desplazamiento opuesto al que debería producir la fuerza eléctrica, el trabajo eléctrico será un valor negativo.

El trabajo eléctrico de una fuerza eléctrica siempre será positivo salvo que intervenga alguna fuerza externa que provoque un desplazamiento opuesto al que debería provocar únicamente la fuerza eléctrica.

Trabajo de Fuerzas Externas contrarias a la Fuerza Eléctrica

El trabajo eléctrico es el trabajo que realizan las fuerzas eléctricas, pero ¡no te confundas!. Otra cosa distinta es el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). En este caso, el trabajo realizado por dicha fuerza externa para mover un cuerpo desde un punto A a otro B es:

We=−Wf

donde:

• We es el trabajo realizado por la fuerza eléctrica para moverlo desde A hasta B.
• Wf es el trabajo realizado por la fuerza externa para moverlo desde A hasta B.

Bibliografia:

https://www.fisicalab.com/apartado/intro-trabajo-electrico#contenidos